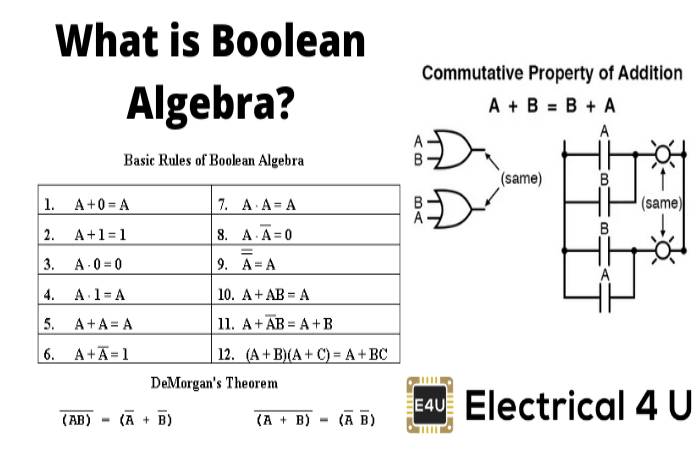
In Boolean Algebra The Bar Sign Indicates
Huh. Boolean algebra is the math we use to analyze digital gates and circuits. As well as utilizing the logic symbols “0” and “1” to represent digital inputs or outputs, we can also use them as constants for “open” or “closed” circuits or contacts, respectively.
In modern Boolean algebra, we have the plus (+) symbol or the dot (•) symbol meaning and the bar Above A Variable Definition. In Boolean Algebra The Bar Sign Indicates
Boolean Algebraic Theorems
De Morgan’s Theorem :
Transposition Theorem :
Proof: RHS = (A + C) (A’ + B) = AA’ + A’C + AB + CB = 0 + A’C + AB + BC = A’C + AB + BC(A + A’) = AB + ABC + A’C + A’BC = AB + A’C = LHS.
Example: AB + BC’ + AC = AC + BC’
Table of Contents
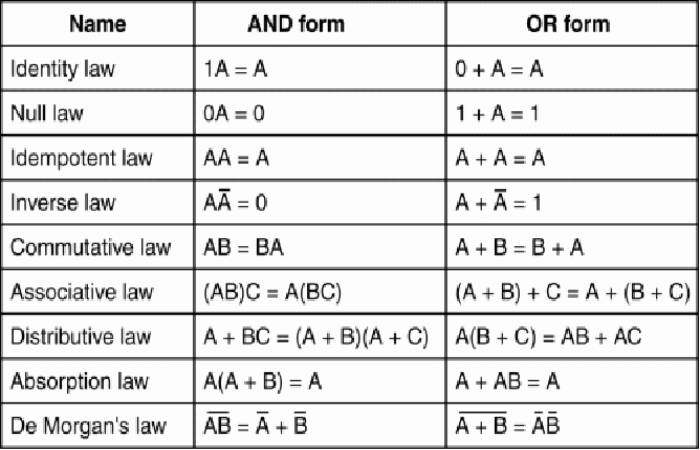
Basic Properties In Boolean Algebra The Bar Sign Indicates
In short, there are three basic properties
- Commutative
- Associative
- Distributive
The first Boolean identity is that the sum of anything and zero is the same as the original “anything.” This identity is no different from its real-number algebraic counterpart: whatever the value of A, the output will always be the same: when A=1, the result is also 1; When a = 0, the work will also be 0.
What is the Importance Of Boolean Algebra?
Today, Boolean algebra is essential to probability, the geometry of sets, and information theory. Furthermore, it is the basis for the design of circuits used in electronic digital computers.
Other examples of Boolean algebras arise from topological spaces: if X is a topological space, then the collection of all subsets of X that are both open and closed forms a Boolean algebra with the operations:= (union) and:= (intersection).
In simple algebra, letter signs take on any number of values. Boolean algebra takes on two values, i.e. 0 and 1. Values assigned to an adjustable have numerical significance in ordinary algebra, whereas they have logical energy in Boolean algebra.
A complementary distribution lattice is known as a Boolean algebra. It is represented by (b, ,∨,’,0,1), where b is a set on which two binary operations (*) and (+) and one unary operation (complement) are defined. Here 0 and 1 are two different elements of B.
The basics of Boolean algebra are generally reasonably easy to pick up. Then the learning curve becomes a bit steep. A big part of this is that it is pretty abstract. Your best bet is to decide which strategies and approaches will help you better see and understand what is going on.
Who Invented Boolean Algebra?
George Boole
George Boole (born November 2, 1815, Lincoln, Lincolnshire, England—December 8, 1864, Ballintemple, County Cork, Ireland), the English mathematician who helped establish modern symbolic logic and whose algebra of logic, now known as Boolean Algebra, called algebra, is essential to the design of digital computer circuits.